Last week I stumbled upon this article, and tweaking my decks to better fit this template has made them run SO MUCH smoother. Of course I wasn’t running enough lands, and my curves weren’t as tight as they could be.
The idea behind this template is to curve out the best you can, with the assumption that games end at turn 7.
The template also assumes that you want to play your commander as fast as possible, which is why there is no spell at the mv of your commander in the curve. This also means that if you play a commander with a mana value of less than 4, you shouldn’t play 2mv-ramp spells (like signets), because it would throw off your curve. If your commander has a mana value of 3, ramping on turn 2 won’t make you cast it faster, so you better spend your mana on something else.
Remember that this is only a template, and it does not cover every possible type of deck. My Aesi landfall deck runs 43 decks instead of the 38 recommended by the template (and should probably run even more), while my Veyran storm deck only runs 31 (but has lots of cheap card draw and plays MDFC cards). For these edge cases I recommend you this article by the same guy, where he explains in more details the formula he used to create this tempate. He also wrote an article about how many color sources you should run to consistently cast colored spells, but none of my decks have more than two colors so I can’t talk to quality of it.
Hope this is as informative to you as it was to me !

Show me the math already! A hypergeometric distribution is the statistical tool of choice this time. The first card you draw is always simple: if you have 40 lands and 99 cards the chance of drawing a land is 40/99. But what about after that? If you didn’t draw a land the probability is 40/98 but if you did it’s 39/98. How does that work? Hypergeometric distributions (Wikipedia article) describe this behaviour nicely when you’ve got a single variable. You need the following information: total number of cards, cards drawn, number of desired cards in the deck, and number of desired cards in the hand. Here’s a tool you can use: the Aetherhub tool. The formula spits out a probability of the desired event happening, where “event” means for example “you drawing 3 lands in your opening 7 when you’ve got a deck of 99 cards with 40 lands in it”.
There’s a problem, though. What if we have lands and ramp we want to consider? Introducing multivariate hypergeometric distributions. A powerful tool that can have any number of variables. For example we could consider the probability of “you drawing 3 lands and 1 ramp spell and 1 draw spell in your opening 7 when you’ve got a deck of 99 cards with 40 lands in it”. Multivariate hypergeometric distribution is what we’re going to use. We’ve got two variables in this study: number of lands and number of ramp. We assume that the third category is “other spells” and none of these categories overlap (they’re mutually exclusive). This puts things like [[Ancient Tomb]] in a weird spot because it belongs in two different categories simultaneously but we’ll just blatantly ignore it.
Calculating the probability of a good hand We take P(2 lands, 1 ramp), P(2 lands, 2 ramp), P(3 lands, 0 ramp), and P(3 lands, 1 ramp) and we add those together to get P(good hand).
The way each calculation takes place is somewhat straightforward. In mathematics there is a concept called “combination” (Wikipedia article) which is what we’re going to use since most programs don’t understand multivariate hypergeometric distributions. It’s written generally as “n choose k” where n is the total population of the item in question and k is the number of items in a subset. The number that is spat out is the number of combinations there can be. For example 3 choose 2 would be 3 because there are 3 different combinations of two numbers that can be represented with three numbers. Imagine an apple, an orange, and a pear. You can have an apple and an orange, an apple and a pear, or an orange and a pear - three combinations. Spreadsheet programs know combinatiorials by the function name “COMBIN(n,k)”.
The formula for a multivariate hypergeometric distribution is the following: (lands choose desired number of lands in hand) x (ramp choose desired number of ramp in hand) x (the others choose desired number of other cards in hand) and the whole thing is divided by all the possible starting hands in EDH which is 99 choose 7. (Which is, by the way, a pretty big number.) The resulting number is the probability of drawing such a hand.
Mulligans Mulliganing in this case is easy. It’s a bit of math but bear with me.
For the first hand it’s just P(1st hand is good).
For the first mulligan since we’re after the total chance we’ll have P(1st is good) or P(1st is bad and 2nd is good) which is the same as P(1st is good) + P(1st is bad) x P(2nd is good).
Via complement this is the same as (1 - P(1st is bad)) + P(1st is bad) x (1 - P(2nd is bad)) which is the same as 1 - P(1st is bad) + P(1st is bad) - P(1st is bad) x P(2nd is bad).
Since between mulligans we always shuffle the deck these events are not dependent on each other i.e. they’re independent. They’re the same thing. Thus P(2nd is bad) is actually also P(1st is bad). At this point we’re at 1 - P(1st is bad) + P(1st is bad) - P(1st is bad)^2.
This all nicely cancels itself out to the form 1 - P(1st is bad)^2 where “2” is actually the number of hands we’ve seen thus far. For the second mulligan it’s 1 - (1st is bad)^3 and so forth.
Opening hand breakdown Here are the coveted charts - the first one is for the case of no mulligans and the second one is with three mulligans.
On the chart you see a heat map. The leftmost column represents the number of lands and the topmost row represents the number of ramp spells. The percentages you see in the middle are the chance of you succeeding in drawing a good hand as outlined earlier.
Each probability you see on the first heat map is for just the opening hand. Each probability you see on the second heat map is for three mulligans, i.e. down to 5 cards. It’s an arbitrary number but as you can see from the percentages it’s pretty rare that we’d have to mulligan any further. Plus keeping a 4 card hand is not very lucrative because you need some lands and ramp but you don’t really have any space for gas. You can also go ahead and keep a mana rich hand (e.g. a 4 land hand) and bottom some mana sources you don’t need in the later mulligans so that increases your chances of finding a keepable hand significantly.
You can read the charts in many ways. The most obvious takeaway is the “optimal” composition at 36 lands and 12 ramp spells because the percentage of drawing into a successful hand is the highest at that point. Isn’t that what people usually recommend?
One can also use it in two other ways: given that you have an X amount of lands or ramp how many of the other type should one run for the best results? The third way is to decide on a percentage you’re willing to get screwed over and look up compositions that have the same number.
A small nod to further draws If we play 36 lands and 12 ramp spells our chance of drawing either a land or a ramp card as your first draw is a little under 50% (48/99). Over the course of the game this percentage should stay about the same regardless of how many cards we draw if we assume you’re not an outlier i.e. being mana screwed or mana flooded. This roughly means that when you run out of mana in your opening hand (by turn 2 or 3) you will have drawn about 1-1.5 new sources. Play those too and you’re looking at a total of 1.5-2 additional sources before you run out of mana sources completely.
Since finding a 4-mana opening hand rather than a 3-mana one is the more common option out of the two we can mostly assume that most decks will get to their magical 6 mana somewhat on curve, depending on luck. After that you’ll get a mana source every second turn or so.
Limitations We’ve covered most of these on the way here but here’s a recap.
This study only optimises your starting hand. It does not know anything about the future draws.
A deck contains 99 cards, a certain number of ramp spells and lands. These categories do not overlap and the calculations for example don’t take into account the possibility of keeping a mana rich hand where one of the lands is actually a MDFC. Or Ancient Tomb.
An opening hand is 7 cards. Mulligans are London mulligans. We mulligan a maximum of 3 times - i.e. at worst you tuck 2 cards from your hand.
A ramp spells can only have mana values of 0, 1, or 2. This means that you can’t really use the chart to figure out your available mana on the early turns because an Arcane Signet and [[Mana Crypt]] are of the same value in this study.
A keepable hand is on of the following: 2 lands and 1 ramp spell, 2 lands and 2 ramp spells, 3 lands, or 3 lands and 1 ramp spell. You might keep a different kind of a hand depending on the specific circumstances but they’re not worth optimising for.
An additional variable would add a dimension making the data representation nearly impossible.
This tool breaks when you start drifting away from that average mana value of 3. This can be clearly seen in cEDH where a starting hand wouldn’t look like the ones we drew. The scope of this study is not cEDH or ultra high mana value decks.
Conclusions Given our assumptions about an optimal hand the ideal amount of lands is 36 and the ideal amount of ramp is 12 spells. These numbers yield a very high chance of drawing into a good hand but small deviations from those numbers are usually almost as good. Can you cut a land for a cool new spell? Sometimes!
Future considerations One could argue that the opening hand isn’t the most important aspect. In fact it could be hitting that magical 6 or 7 mana. The math gets a bit complicated because one needs to still decide what is a good opening hand, do mulligans and after all that draw the necessary cards to see how well a hand fares.
Feedback, please Did I make any mistakes? The math has been verified by a handful of people (hence “we” in the text) but there’s always a chance we all overlooked something. Did you enjoy this? Is it going to be helpful for you?
UPDATE Judging by the general feel of it I’m publishing one more chart. This chart here optimises additionally for 4 land hands, too. The formula I’m using breaks at 0 and 1 ramp spells and I can’t be bothered to fix that because it’s just an afterthought but as you can see if we optimise for these five opening hands:
2 lands, 1 ramp spell
2 lands, 2 ramp spells
3 lands, 0 ramp spells
3 lands, 1 ramp spell
4 lands, 0 ramp spells
the whole chart shifts dramatically to favour lands. The chart is for no mulligans (mulliganing doesn’t change the optimum). It does make more hands keepable increasing the chance of getting “a good hand” but it warps the chart a lot.
This is one of the reasons why I did not include 4 land hands in the first place. The “ideal” would now be around 48-49 lands and about 0 ramp spells which does not make sense in the slightest. It doesn’t reflect the power of ramp spells properly at all. All in all while 4 land hands may be keepable they’re not really worth optimising for.
SECOND POST:
My commander costs 4 mana. How many lands and ramp spells do I need to get it out on turn 3? TL;DR: 37 lands and 15 ramp spells at mana value 2 or less.
This short analysis is a continuation to “I’ll just cut a land”: A statistical analysis of lands and ramp in EDH article that was published 7 months ago. Also provocative title: I’m not saying this is the absolute truth but I’m putting forth the idea that every deck does need enough mana sources to play the game. This article discusses 4 mana commanders being cast ahead of curve.
I was building a new deck, helmed by Rosheen Meanderer (scryfall). The thing about Rosheen X-creatures is that I need Rosheen out as soon as possible (turn 3 or earlier). My prior advice was 36 lands and 12 ramp spells (see the other Reddit article) but I was left wondering if that’s enough to get Rosheen out on turn 3. Answer: it’s not.
This time I used a bit more complicated method of simulating the game to turn 2 assuming we’re not playing any draw/loot/filter/rummage spells in the first two turns (which is true for my deck). The “simulation” here is simply to see a decent hand and hope our next two draws are good.
Why turn 2? If you play a Rampant Growth on turn 2 you can still cast your 4-mana commander on turn 3. If your 3rd draw is a Rampant Growth, however, it doesn’t help you at all. Thus we need to cast all our ramp spells by turn 2. This also incidentally means that your ramp at mana value 3 or above doesn’t help you cast your commander at all so you shouldn’t count those towards ramp in your deck when it comes to this analysis. Cultivate is a decent card but exclude it this time.
The math is based on opening hands. Here’s a table of hands and early draws I deemed acceptable:
opening 7 lands opening 7 ramp first 2 draws lands first 2 draws ramp 2 1 1 or 2 0 or 1 2 2 1 or 2 0 3 0 0 or 1 1 or 2 3 1 0 or 1 0 or 1 3 2 0 or 1 0 4 0 0 1 or 2 4 1 0 0 or 1 The philosophy here was that I draw a relatively safe hand and taking the two draws into account we’re looking at 4 mana on turn 3. In other words that’s our “mana target”. There may also be a surplus left over since drawing into 4 lands is not necessarily a bad thing looking into the future. Looking at a 5 land opener can be a good thing but if there’s a ramp spell in it it means we’ve only got one more spells that we can play (7-5-1=1). Doesn’t sound nice to me. But in general I don’t mind an extra land or ramp spell to be cast on turn 4. Feel free to disagree with my “safe” openers.
Obviously we can’t know the future draws so they only act as “weight factors” for each hand. If you draw into a land rich hand with no ramp you absolutely need that one ramp spell. While we’re optimising for a land rich hand by including it in the table we also take into account the fact that there must be a ramp spell in the next two cards which in turn increases the number of ramp spells needed in the deck so they kind of counteract each other.
Think of it this way: 3 lands and 1 ramp is a very, very safe hand. If it can accept any outcome from future draws it’s the “best” opener possible. It gets a weight of 1 because the probability of drawing any (follow-up) card from your deck is always 1. If your hand is 2 lands and 1 ramp spell your hand must draw an extra land to survive - draws with no lands are bad so we exclude them and thus lower the weight of the hand in terms of overall optimisation. This way the math prefers the safest hands and gives them a higher priority.
Here’s a cool heat map. Look at it. It’s amazing. This heat map describes the probability of drawing a good opener and then having two favourable draws on turns 1 and 2. Each cell simply means “probability of happy times”. From it you can see that the optimum is 38 lands and 16 ramp spells but the probability doesn’t decrease significantly if you go to 37 lands and 15 ramp spells (hence the title of the post). This is surprising because the old adage is that your deck should have about 36 lands and 10 ramp spells in it for a total of 46 mana sources (my recommandation in the previous article was 36 and 12 for a total of 48). While it’s close to that you may want to look at your deck critically and think if you need more than 50 sources. If you don’t care about casting your commander on turn 3 then go with something lower. The “midpoint” of the colour scale is set to 85th percentile, by the way. So roughly green is good.
In more detail: each cell takes the probability of finding a particular kind of opener (outlined in the table above) and then multiplies that (the AND condition in probabilities) by the probabilities of good outcomes and then adds all the hands together (the OR condition in probabilities) to produce a single probability table. Each cell has a bunch of multivariate hypergeometric functions (not the simple kind) - it’s a bit cumbersome so if you want more details about this you must contact me directly.
Fun fact: the table contains 11250 calculations where each calculcation has a number that is in the ballpark of 10 billion (American notation; 1010 for the more scientific minded people). It takes a few minutes to render the entire table.
Thank you for reading, hope this helps you somehow! Always take a stranger’s word with a pinch of salt and feel free to disagree in the comments.
Images:
No mulligans, general advice (first post):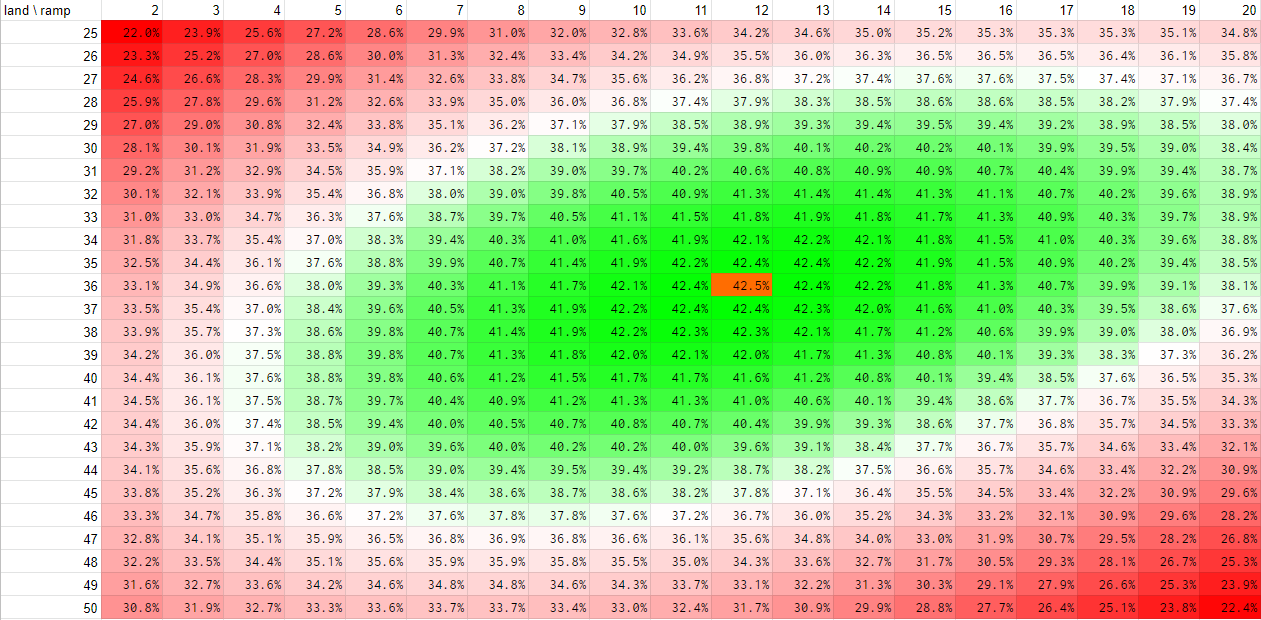
Three mulligans, general advice (first post):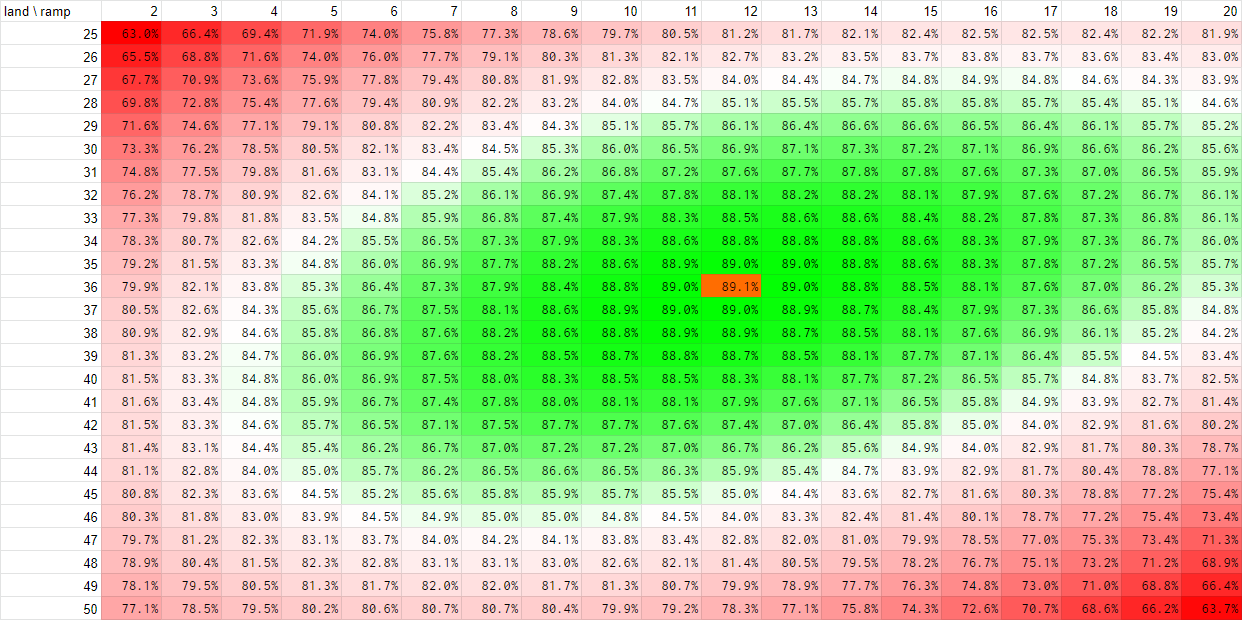
Accepting 4 land hands, general advice (first post):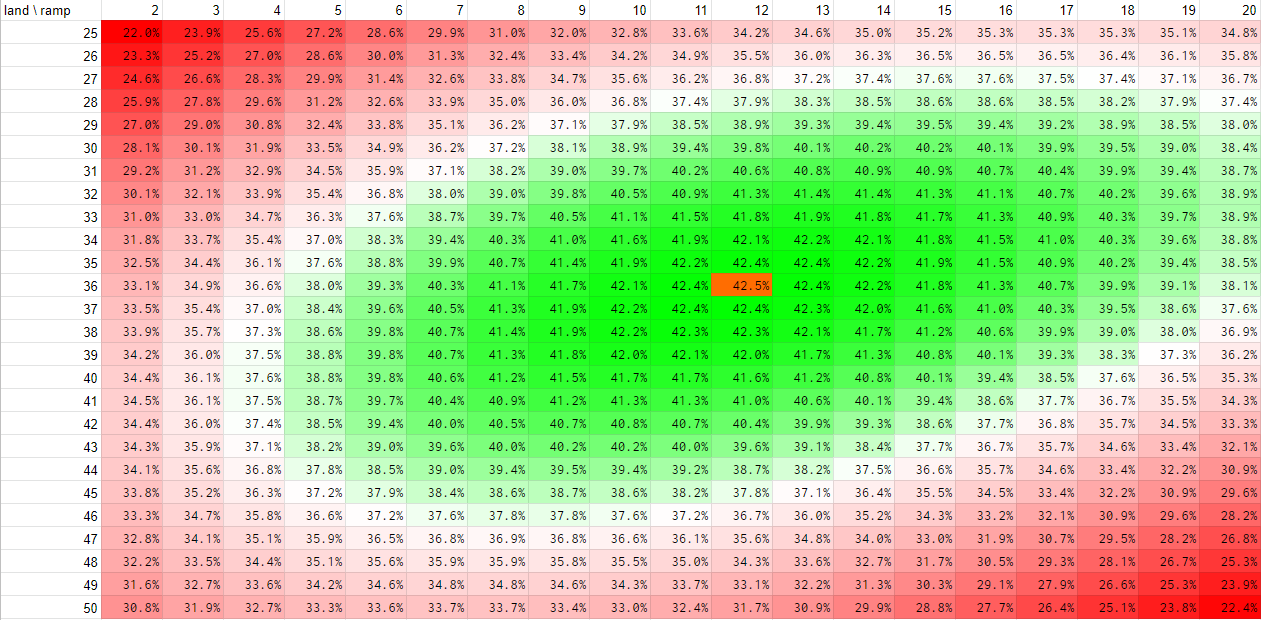
4-mana commander (second post):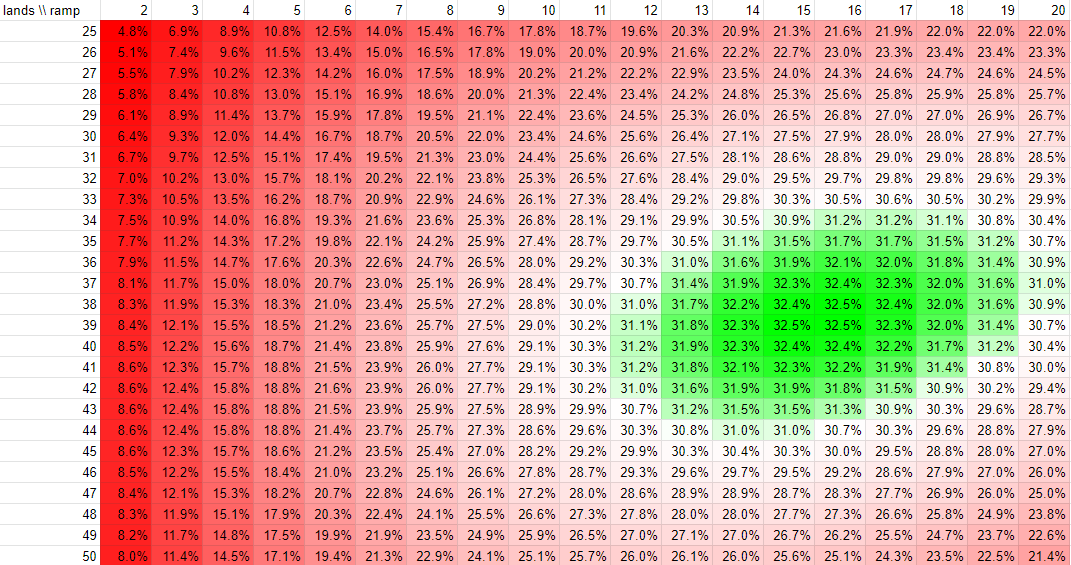
Wow that’s a thorough analysis ! Thanks a lot. It does cover a blind spot of the article, which is that it is based on what people are doing instead of what they should do. I will experiment with your model !
15 cheap ramp spells feels like a tall order if you don’t run green though, especially if you don’t have the budget for mana crypt/mana vault/moxes.
Do you have an idea of how fast the output of your model changes when the average cmc of the deck changes ?
Crap, I wrote a long comment and accidentally closed the tab. Well.
In a nutshell: 15 ramp spells is doable. There are already 15 colourless rocks to fulfill this order.
So the analysis above doesn’t take average mana value into account. It simply looks at the (subjectively) acceptable starting hands and goes from there. You can indirectly manipulate the assumed average mana value by modifying which hands to accept and which to mulligan.
I have experimented with a variable MV setup… But the results are pretty wild. I’ll return to you if I ever get around to doing some more of that. (Yeah, that’s going to be tonight lol.)
[[card name]] to call
[[card name]] to call